Question

close sidebar webwork/mat145f19stern/hw13/5 HW13: Problem 5 Previous Problem Problem List Next Problem (1 point) A parcel delivery service will deliver a package only if the length plus the girth (distance around, taken perpendicular to the length) does not exceed 104 inches. Find the maximum volume of a rectangular box with square ends that satisfies the delivery company's requirements.

Answer 1

The volume in such a package is 10,415.41 in³

Explanation:

Consider the provided information.

A parcel delivery service will deliver a package only if the length plus the girth (distance around, taken perpendicular to the length) does not exceed 104 inches.

Let the dimension are x by x by y.

Where x is the variable for the square base package and y is the variable for length.

Thus l=x, b=x and h=y

Then the volume of the box is:
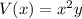`V(x)=x^2y` (∵V=lbh)

The maximum combined length and girth is 104.

Therefore,
`4x+y=104`

`y=104-4x`

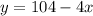
Substitute the value of y in volume of the box.

`V(x)=x^2(104-4x)`

`V(x)=104x^2-4x^3`

`V'(x)=208x-12x^2`

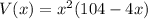
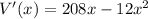
Substitute V'(x)=0.

`0=208x-12x^2`

`-4x(3x-52)=0`

`x=0\ or\ x=(52)/(3)`

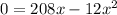
Now apply second derivative test.

`V''(x)=208-24x`

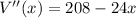
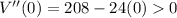`V''(0)=208-24(0)>0` (Min)

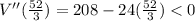`V''((52)/(3))=208-24((52)/(3))<0` (Max)

If x=52/3 then
`y=104-4((52)/(3))=(104)/(3)`

Substitute x = 52/3 and y = 104/3 in
`V(x)=x^2y`

`V(x)=((52)/(3))^2* (104)/(3)=10,415.41`

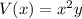
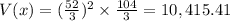
Hence, the volume in such a package is 10,415.41 in³