Answer:
A)
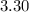 ms⁻¹
ms⁻¹
B)
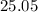 J
J
C)
i)
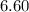 ms⁻¹
ms⁻¹
ii)
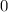 ms⁻¹
ms⁻¹
iii)
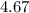 ms⁻¹
ms⁻¹
Step-by-step explanation:
A)
 = velocity of center of hoop
= velocity of center of hoop
w = angular speed of the hoop = 3 rads⁻¹
d = diameter of the hoop = 2.20 m
radius of the hoop is given as
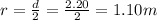
velocity of center of hoop is related to angular velocity by the relation given as
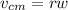
inserting the values
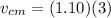
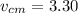 ms⁻¹
ms⁻¹
B)
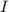 = moment of inertia of hoop
= moment of inertia of hoop
 = mass of the hoop = 2.30 kg
= mass of the hoop = 2.30 kg
 = radius of hoop = 1.10 m
= radius of hoop = 1.10 m
Moment of inertia of the hoop is given as
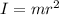
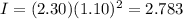 kgm²
kgm²
Total kinetic energy is given as
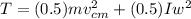
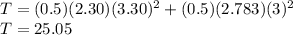 J
J
C)
i)
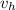 = velocity at highest point
= velocity at highest point
velocity at highest point is given as
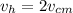
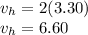 ms⁻¹
ms⁻¹
ii)
 = velocity at bottom
= velocity at bottom
velocity at bottom point is given as
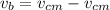
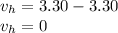 ms⁻¹
ms⁻¹
iii)
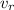 = velocity at right
= velocity at right
velocity at right is given as
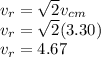 ms⁻¹
ms⁻¹