Answer:
-3
Explanation:
Given that an insurance policy reimburses a loss with a deductible of 5. That is, if a loss is less than 5, policy will pay zero. If it is more than 5, then the policy will pay (loss - 5).
We have distribution of y as
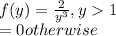
expected value of the benefit paid under the insurance policy
=
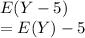 , by linearity property of expectation.
, by linearity property of expectation.
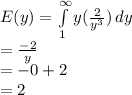
Hence expected value of the benefit paid under the insurance policy
=2-5 =-3