Question

12) Add the fractions, and simplify if possible.

(y+7)/(y^2-y-12) - 2/(y^2-9)

Answer 1

`(y^2+2y-13)/((y-4)(y+3)(y-3))`

Explanation:

Given the expression

`(y+7)/(y^2-y-12)-(2)/(y^2-9)`

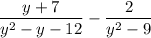
First, factor each denominator:

1.
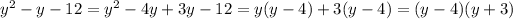
`y^2-y-12=y^2-4y+3y-12=y(y-4)+3(y-4)=(y-4)(y+3)`

2.
`y^2-9=(y-3)(y+3)`

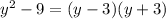
Now the expression is

`(y+7)/((y-4)(y+3))-(2)/((y-3)(y+3))`

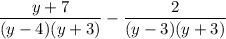
Now, multiply the first numerator by (y-3) and the second by (y-4) and write the result as a fraction with denominator
`(y-4)(y+3)(y-3):`

`((y+7)(y-3)-2(y-4))/((y-4)(y+3)(y-3))=(y^2-3y+7y-21-2y+8)/((y-4)(y+3)(y-3))=(y^2+2y-13)/((y-4)(y+3)(y-3))`

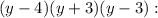
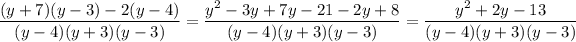
This fraction cannot be simplified more.