Question

Suppose that prior to conducting a coin-flipping experiment, we suspect that the coin is fair. How many times would we have to flip the coin in order to obtain a 90% confidence interval of width of at most .18 for the probability of flipping a head?a) 83b) 84c) 87d) 50e) 51f) None of the above

Answer 1

Answer: b) 84

Explanation:

Let p be the prior estimate of the required proportion.

As per given , we have

p =0.5 (The probability of getting heads on a fair coin is 0.5)

Significance level :
`\alpha: 1-0.90=0.10\\`

Critical z-value (using z-value table ) :
`z_(\alpha/2)=1.645`

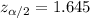
Confidence interval width : w= 0.18

Thus , the margin of error :
`E=(w)/(2)=0.09`

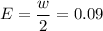
Formula to find the sample size ( if prior estimate of proportion is known.):-

`n=p(1-p)((z_(\alpha/2))/(E))^2`

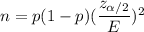
Substitute the values , we get

`n=0.5(1-0.5)((1.645)/(0.09))^2`

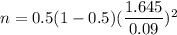
Simplify ,

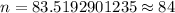`n=83.5192901235\approx84` [Round of to the next whole number.]

Hence, the number of times we would have to flip the coin =84

hence, the correct answer is b) 84