Question

A flocculation basin equipped with revolving paddles is 60 ft long (the direction of flow). 45 ft wide, and 14 ft deep and treats 10 mgd. The power input to provide paddle-blade velocities of 1.0 and 1.4 fps for the inner and outer blades, respectively, is 930 ft'lb/s. Calculate the detention time, horizontal flow-through velocity, and G (the mean velocity gradient) for a water temperature of 50'F.

Answer 1

detention time = 40.72 minutes

horizontal velocity v = 0.295 inch/s

mean velocity gradient, G = 54.38
`s^(-1)`

Step-by-step explanation:

given data

long = 60 ft

wide = 45 ft

deep = 14 ft

flow of water to treat = 10 mgd = 15.472 ft³/s [1 MGD = 1.5472 ft³/s ]

inner velocities = 1.0 fps

outer velocities = 1.4 fps

power required to rotates the paddles = 930 ft-lb/s

solution

we find detention time that is

time =
`(V)/(Q)`

here Q = flow of water and V is volume of water

so

volume of flocculation basin is = 60 × 45 × 14 = 37800 ft³

so

detention time =
`(37800)/(15.472)`

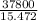
detention time = 40.72 minutes

and

horizontal flow through velocity is

cross-section area of tank = 45 × 14 = 630 ft²

and we know that Av = Q

so horizontal velocity v =
`(Q)/(A)`

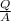
horizontal velocity v =
`(15.472)/(630)`

horizontal velocity v = 0.02456 ft/s

horizontal velocity v = 0.295 inch/s

and

now we find mean velocity gradient G at temperature of 50'F

so formula is G =
`\sqrt{(P)/(\mu V) }`

here P is power input and μ is viscosity and V is volume of flocculation basin

so Volume of flocculation basin is 37800 ft³

and μ for 500F = 8.3197 ×
`10^(-6)` lb-s/ft²

we take from table

so we get

G =
`\sqrt{(930)/(8.3197*10^(-6)*37800) }`

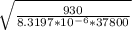
mean velocity gradient, G = 54.38
`s^(-1)`