Answer:
We can conclude that the mean time is greater than 10 minutes.
Explanation:
In this case we have to perform a hypothesis testing of the mean, with standard deviation of the population unknown.
The conclusion we have to demonstrate with evidence is that the mean is greater than 10 min, so the null and alternative hypothesis became:
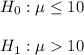
The significance level is 0.05.
The test statistic is
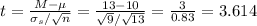
For a sample size of n=13, the degrees of freedom are 13-1=12. We can look up in a t-table the P-value for a t=3.614 and df=12.
The P-value is 0.00178. As the P-value is less than the significance level, we can conclude that the effect is significant and the null hypothesis is rejected.
We can conclude that the mean time is greater than 10 minutes.