Step-by-step explanation:
A "reduced" fraction is one that has mutually prime numerator and denominator. That is, the numerator and denominator have no common factors.
A fraction is "reduced" by canceling common factors from numerator and denominator. If "a" is a factor common to the numerator and denominator of a fraction, that fraction can be written with "a" canceled from each:
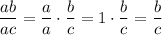
Here is a numerical example:
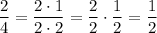
__
A numerator factor and a denominator factor "cancel" because their ratio is 1, the identity element for multiplication. Anything times 1 is just that thing.