Question

Suppose that 20% of the residents in a certain state support an increase in the property tax. An opinion poll will randomly sample 400 state residents and will then compute the proportion in the sample that support a property tax increase. How likely is the resulting sample proportion to be within 0.04 of the true proportion (i.e., between 0.16 and 0.24)? (Hint: Use the sampling distribution of the sample proportion in this case.)

A) It is certain that the resulting sample proportion will be within 0.04 of the true proportion.
B) There is roughly a 99.7% chance that the resulting sample proportion will be within 0.04 of the true proportion.
C) There is roughly a 95% chance that the resulting sample proportion will be within 0.04 of the true proportion.
D) There is roughly a 68% chance that the resulting sample proportion will be within 0.04 of the true proportion.

Answer 1

C) There is roughly a 95% chance that the resulting sample proportion will be within 0.04 of the true proportion.

Explanation:

Given that 20% of the residents in a certain state support an increase in the property tax.

Sample size = 400

We want the sample proportion to be within 0.04 of the true proportion (i.e., between 0.16 and 0.24)

i.e. margin of error <0.04

Std error of sample =
`\sqrt{(pq)/(n) } =\sqrt{(0.2(0.8))/(400) } \\=0.02`

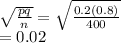
Critical value = margin of error/ std error =
`(0.04)/(0.02) \\=2`

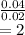
We know z value for 95% two tailed roughly equals 2.

Hence 95% confidence is right.

C) There is roughly a 95% chance that the resulting sample proportion will be within 0.04 of the true proportion.