Question

A 2,200 kg railway freight car coasts at 3.6 m/s underneath a grain terminal, which dumps grain directly down into the freight car. If the speed of the loaded freight car must not go below 3.1 m/s, what is the maximum mass of grain (in kg) that it can accept?

Answer 1

`m_2=2554.83\ kg`

Step-by-step explanation:

Given that,

Mass of the car,
`m_1=2200\ kg`

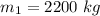
Initial speed of the car,
`u=3.6\ m/s`

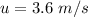
Final speed of the car,
`v=3.1\ m/s`

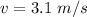
To find,

The maximum mass of grain that it can accept.

Solution,

We know that according to the law of conservation of momentum, the initial momentum is equal to the final momentum.

`m_1u=m_2v`

`m_2=(m_1u)/(v)`

`m_2=(2200* 3.6)/(3.1)`

`m_2=2554.83\ kg`

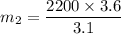
Therefore, the maximum mass of grain that it can accept is 2554.83 kg. Hence, this is the required solution.