Answer:
27h
Step-by-step explanation:
We can answer this problem with Kepler's third law:
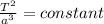
where
 is the period and
is the period and
 is the semi-major axis of an ellipse, but because the satellite's orbit is around the earth it must be a circular orbit, so that
is the semi-major axis of an ellipse, but because the satellite's orbit is around the earth it must be a circular orbit, so that
 becomes the radius
becomes the radius
 of a circle.
of a circle.

what this tells us is that the relationship between the first period with radius
 must be equal to the second period when the radius is now 9 times the original (the second radius is
must be equal to the second period when the radius is now 9 times the original (the second radius is
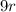 because the orbit is nine times larger):
because the orbit is nine times larger):
We will have the following:
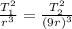
 is the original period: 1 hour
is the original period: 1 hour
 is the period of the second satellite.
is the period of the second satellite.
and
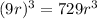
thus:
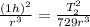
Clearing for

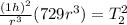
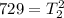
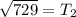
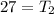
The period of the second satellite is 27 hours