Question

CX Enterprises has the following expected​ dividends: $ 1.05 in one​ year, $ 1.24 in two​ years, and $ 1.35 in three years. After​ that, its dividends are expected to grow at 4.1 % per year forever​ (so that year​ 4's dividend will be 4.1 % more than $ 1.35 and so​ on). If​ CX's equity cost of capital is 11.7 %​, what is the current price of its​ stock?

Answer 1

$16.16

Step-by-step explanation:

Given that,

Expected​ dividends:

$1.05 in one​ year, D1

$1.24 in two​ years, D2

$1.35 in three years, D3

Growth rate of dividend, g = 4.1%

Equity cost of capital, e = 11.7 %​

`P3=(D3(1+g))/((e-g))`

`P3=(1.35(1+0.041))/((0.117-0.041))`

`P3=(1.40535)/(0.076)`

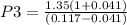
= 18.49

`current\ price=(D1)/((1+e))+(D2)/((1+e)^(2) )+(D3)/((1+e)^(3) )+(P3)/((1+e)^(3) )`

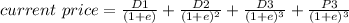
`current\ price=(1.05)/((1.117))+(1.24)/((1.117)^(2) )+[(1.35)/((1.117)^(3) )+(18.49)/((1.117)^(3) )]`

= 0.94 + 0.99 + 14.23

= $16.16