Question

g A company that produces cell phone batteries claims their new battery last more than 30 hours. To investigate this claim a consumer advocacy group collected the following random sample for number hours that each battery worked: 50, 40, 35, 25, 60, 45, 30, 50, 30, 10. Is there a sufficient evidence to accept the company’s claims using 0.01 significance level?

Answer 1

There is no enough evidence to accept the company's claim.

Explanation:

We have a sample of data: 50, 40, 35, 25, 60, 45, 30, 50, 30, 10.

This sample is size n=10 and has a mean of 37.50 and a standard deviaition of 14.57.

The claim of the company is that their new battery last more than 30 hours. We will state that in the alternative hypothesis, and see if there is enough evidence to reject the null hypothesis.

The null and alternative hypothesis are:

`H_0: \mu\leq30\\H_1: \mu>30`

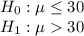
The significance level is 0.01.

The test statistic can be calculated as

`t=(M-\mu)/(\sigma_s/√(n))= (37.5-30)/(14.57/√(10) ) =(7.50)/(4.61)=1.63`

The degrees of freedom for a n=10 size sample are df=10-1=9 degrees of freedom. We can look up in a t-table the P-value for a t=1.63 and df=9 for a one-tailed test.

The P-value is P=0.06877.

This P-value is grater than the significance level, so the effect is not significant and the null hypothesis can't be rejected. There is no enough evidence to accept the company's claim.