Answer:
t=5.4 and t=0.6.
Explanation:
The height of the ball (in feet) after time t is defined by the function
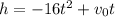
where,
 is initial velocity.
is initial velocity.
It is given that a man throws a ball into the air with a velocity of 96 ft/s.
Substitute v=96 in the above function.
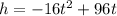
We need to find the time at which the height of ball is 48 feet.
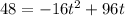
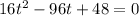 .... (1)
.... (1)
Quadratic formula for
 is
is
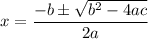
In equation a=16, b=-96 and c=48. Using quadratic formula we get

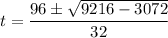
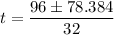
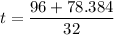 and
and
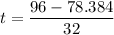
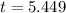 and
and
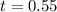
Round the answer to the nearest tenth.
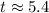 and
and
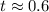
Therefore, the height of ball will be 48 feet at t=5.4 and t=0.6.