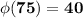Question

The value of the Euler \phi function (\phi is the Greek letter phi) at the positive integer n is defined to be the number of positive integers less than or equal to n that are relativel prime to n, For example for n=14, we have {1, 3, 5, 9, 11, 13} are the positive integers less than or equal to 14 which are relatively prime to 14. Thus \phi (14) = 6.Find the following:\phi(9) = __________.\phi(15) = __________.\phi(75) =__________.

Answer 1

`\bf \phi (9)=5`

`\bf \phi (15)=8`

`\bf \phi (75)=40`

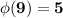
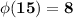
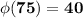
Explanation:

Positive integers relative primes to 9 which are less or equal than 9

{1,2,4,5,7}

so

`\bf \phi (9)=5`

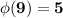
Positive integers relative primes to 15 which are less or equal than 15

{1,2,4,7,8,11,13,14}

and

`\bf \phi (15)=8`

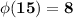
Positive integers relative primes to 75 which are less or equal than 75

{1,2,4,7,8,11,13,14,16,17,19,22,23,26,28,29,31,32,34,37,38,41,43,44,46,47,49,52,53,56,58,59,61,62,64,67,68,71,73,74}

and

`\bf \phi (75)=40`