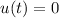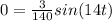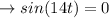This is a Physics problem linked to differential equations.
In order to solve it, we define our initial values:

We have given initial conditions,
The mass starts from a point of displacement at rest, that is,

However, it has a resting point speed equal to 30cm/s
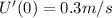
By definition we know that,
By Newton's law we know that
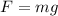
And by Hook's law we know that
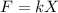
where,
k elongation / elastic constant
X the change or distance traveled
Equating the expressions we have
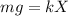
Solving for k,

Replacing,
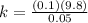
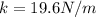
The differential equation given for the movement is,
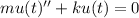
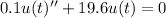
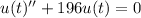
Being a differential equation we can obtain its auxiliary equation, given by
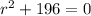
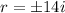
By definition, this is a second order linear differential equation,
We know that every function of the form
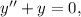 its solution is
its solution is
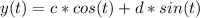
Applying the definition,
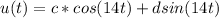
And the first derivative would be
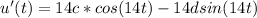
Applying our ideal conditions we can find d and c, so
For u(0) =0
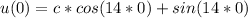
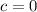
For u(0)=0.3

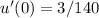
We have know that our equation for the position of the mass at any time is,
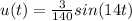
Solving for the question: The time when the mass return to equilibrium we have