Answer:
Explicit formula:

Explanation:
Let the number of squares in
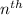 layer be
layer be

Given:
Number of squares in first layer,
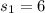
Number of squares in second layer,

Therefore, the number of squares increases by a factor of 2.
So, it follows a geometric sequence with the first term as 6 and common ratio of 2.
For a geometric sequence, the
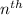 term with common ratio
term with common ratio
 is given as:
is given as:
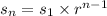
Here,

∴ Explicit formula:
