Question

Consider the quadratic function f(x) = -x^2 + bx - 75.

If the maximum is 25, find the value of b.

Please show the steps!

Answer 1

`b=20`

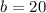
Explanation:

Given:

The quadratic function is
`f(x)=-x^(2)+bx-75`

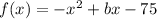
The maximum value of the function is 25.

Comparing it with the standard form,
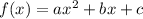`f(x)=ax^(2)+bx+c`, we get

`a=-1,b=b,c=-75`

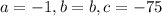
Since,
`a` is negative, we have a downward parabola with maximum value at the vertex.

The vertex of a quadratic function occurs at
`(h,k)=((-b)/(2a),f((-b)/(2a)))`

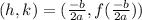
Now,
`h=(-b)/(2a)=(-b)/(-2)=(b)/(2)`

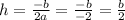
As per question,
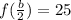`f((b)/(2)) = 25`. This gives,

`f((b)/(2))=-((b)/(2))^(2)+b((b)/(2))-75\\25=-(b^(2))/(4)+(b^(2))/(2)-75\\25+75=(b^(2))/(4)\\100=(b^(2))/(4)\\b^(2)=100* 4\\b=√(400)=20`

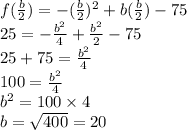
Therefore, the value of
`b` is 20.