Question

A pool has some initial amount of water in it. Then it starts being filled so the water level rises at a rate of 666 centimeters per minute. After 202020 minutes, the water level is 220220220 centimeters. Graph the relationship between the pool's water level (in centimeters) and time (in minutes).

Answer 1

Answer: Points are (20, 220) and (15, 190)

Step-by-step explanation: I had the same quiz question.

Answer 2

`y=6x+100`

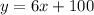
The graph is drawn below.

Explanation:

Let the minutes passed be
`x` and height of water level be
`y` cm.

Given:

Rate of rise of water level,
`m = 6\textrm{ cm/min}`

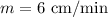
When
`x=20\textrm{ min},y=220\textrm{ cm}`

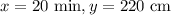
Therefore, the relationship can be expressed using the point-slope form of an equation if a line.

The point-slope form is given as:

`y-y_(1)=m(x-x_(1))`

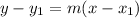
Here,
`m=6,x_(1)=20,y_(1)=220`

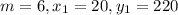
Therefore, the relationship is given as:

`y-220=6(x-20)\\y-220=6x-120\\y=6x-120+220\\y=6x+100`

Therefore, the relationship between the pool's water level (in centimeters) and time (in minutes) is
`y=6x+100`.

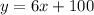The graph is shown below.