Answer:
For minutes less than 50, Verizon's monthly plan will be less expensive then T mobiles.
Explanation:
Let the minutes used be
 .
.
Given:
Cost per minute by Verizon = $ 0.50
∴ Total cost for
 minutes by Verizon =
minutes by Verizon =
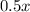
Cost per minute by T mobile = $ 0.10
∴ Cost for
 minutes by T mobile =
minutes by T mobile =
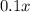
Fixed cost charged by T mobile = $ 20
Therefore, the total cost charged by T mobile =
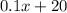
Now, for Verizon cost to be less than T mobile's cost,
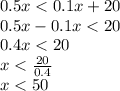
Therefore, for
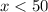 , Verizon's monthly plan will be less than that of T mobile's plan.
, Verizon's monthly plan will be less than that of T mobile's plan.
So, for up to 50 minutes, Verizon's plan is cheaper than T mobile's plan.