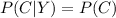Question

Which statement is true about whether C and Y are independent events? C and Y are independent events because P(C∣Y) = P(Y). C and Y are independent events because P(C∣Y) = P(C). C and Y are not independent events because P(C∣Y) ≠ P(Y). C and Y are not independent events because P(C∣Y) ≠ P(C).

Answer 1

D

Explanation:

did the test and got 100%

Answer 2

C and Y are independent events because
`P(C|Y) = P(C)`.

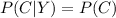Explanation:

Two events X and Y are independent only if

`P(X\cap Y)=P(X)* P(Y)`

Now, if C and Y are independent events, then

`P(C\cap Y)=P(C)* P(Y)`

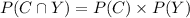
Now, conditional probability of C given that Y has occurred is given as:

`P(C|Y)=(P(C\cap Y))/(P(Y))\\P(C|Y)=(P(C)* P(Y))/(P(Y))\\P(C|Y)=P(C)`

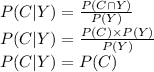
Therefore, two events C and Y are independent because
`P(C|Y) = P(C)`