Question

Flying against the wind, an airplane travels 3060 kilometers in 3 hours. Flying with the wind, the same plane travels 7560 kilometers in 6 hours. What is the rate of the plane in still air and what is the rate of the wind ?

Answer 1

The speed of plane against wind S 1 = 1020 kmph And

The speed of plane with wind S 2 = 1260 kmph

Explanation:

Given as :

The distance of airplane against the wind = D 1 = 3060 km

The time taken in against the wind = T 1 = 3 hours

The distance of airplane with the wind = D 2 = 7560 km

The time taken in with the wind = T 2 = 6 hours

Now, Speed of plane against the wind =
`(Distance)/(Time)`

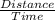
So, S 1 =
`(D 1)/(T 1)`

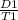
Or, S 1 =
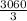`(3060)/(3)` = 1020 kmph

Similarly

Speed of plane with the wind =
`(Distance)/(Time)`

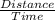
Or, S 2 =
`(D 2)/(T 2)`

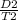
Or, S 2 =
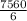`(7560)/(6)` = 1260 kmph

Hence The speed of plane against wind S 1 = 1020 kmph And

The speed of plane with wind S 2 = 1260 kmph Answer