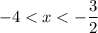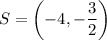Answer:
See below
All the inequalities can be solved by making a table, but once they are simple factored quadratic expressions, we already know what interval it will have.
Explanation:
1)
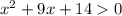
Factoring the expression, we have

Considering that
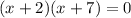
for
 and
and
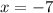 you can see that for
you can see that for


Therefore,
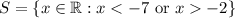
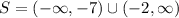
2)
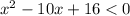
You can factor it again.
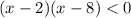
You can make the table to solve all the inequalities, but once we have the expression
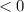 , we know that
, we know that
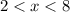 , therefore,
, therefore,
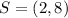
3)
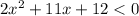
Factoring we have
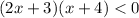
Find the solutions for
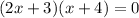
And we know that