Question

One x-intercept for a parabola is at the point

(-0.33,0). Use the quadratic formula to find the
other x-intercept for the parabola defined by
this equation
y=-3x2 + 5x + 2

Answer 1

(2,0)

Explanation:

Given:

The equation is given as:
`y=-3x^(2)+5x+2`

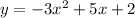
For x intercept,
`y=0`.

Therefore,
`-3x^(2)+5x+2=0`

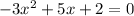
Now, comparing this with the standard quadratic equation
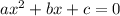`ax^(2)+bx+c=0`, we get

`a=-3,b=5,c=2`

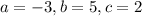
Now, using quadratic formula for the above equation,

`x=\frac{-b \pm \sqrt{b^(2)-4ac}}{2a}\\x=\frac{-5 \pm \sqrt{5^(2)-4(-3)(2)}}{2(-3)}\\x=(-5 \pm √(25+29))/(-6)\\x=(-5 \pm √(49))/(-6)\\x=(-5 \pm 7)/(-6)\\x=(-5-7)/(-6)\textrm{ or }x=(-5+7)/(-6)\\x=(-12)/(-6)\textrm{ or }x=(2)/(-6)\\x=2\textrm{ or }x=-(1)/(3)=-0.33`

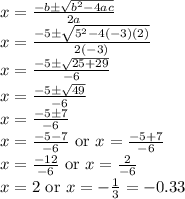
Therefore, there are two x intercepts. One was given as (-0.33,0). So, the other one is (2, 0).