Answer:
(2,0)
Explanation:
Given:
The equation is given as:
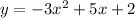
For x intercept,
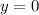 .
.
Therefore,
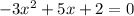
Now, comparing this with the standard quadratic equation
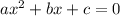 , we get
, we get
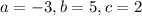
Now, using quadratic formula for the above equation,
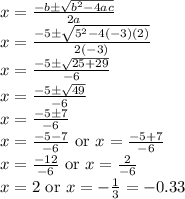
Therefore, there are two x intercepts. One was given as (-0.33,0). So, the other one is (2, 0).