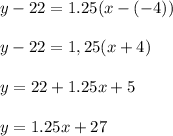Answer:
1.
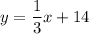
2.
Explanation:
1. The equation of the line passing through the points
 and
and
 is
is
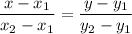
In your case, the line passes through the points (-18,8) and (-9,11). So, its equation is
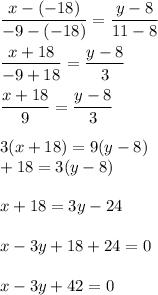
In the slope intercept form this equation is
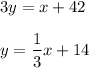
2. First, find the slope of the line
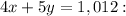
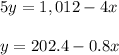
Thus, the slope of this line is
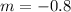
Two perpendicular line have the slopes with their product equal to -1:
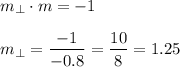
The equation of perpendicular line is
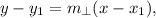
where
 are the coordinates of the point the line passes through. So,
are the coordinates of the point the line passes through. So,