Question

A massive truck of 1200N moving with a velocity of 2m/s hits a stationary mass of 30N. if the both bodies move together after the collision, determine their common velocity.​

Answer 1

The common speed is 1.95 m/s

Step-by-step explanation:

Law Of Conservation Of Linear Momentum

It states that the total momentum of a system of bodies is conserved unless an external force is applied to it. The formula for the momentum of a body with mass m and velocity v is

P=mv.

If we have a system of bodies, then the total momentum is the sum of all of them:

`P=m_1v_1+m_2v_2+...+m_nv_n`

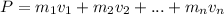
If a collision occurs, the velocities change to v' and the final momentum is:

`P'=m_1v'_1+m_2v'_2+...+m_nv'_n`

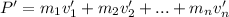
In a system of two masses, the law of conservation of linear momentum

is written as:

`m_1v_1+m_2v_2=m_1v'_1+m_2v'_2`

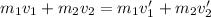
If both masses stick together after the collision at a common speed v', then:

`m_1v_1+m_2v_2=(m_1+m_2)v'`

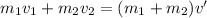
The common velocity after this situation is:

`\displaystyle v'=(m_1v_1+m_2v_2)/(m_1+m_2)`

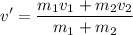
The truck of m1=1200 N (weight) travels at v1=2 m/s and hits a stationary mass (v2=0) of m2=30 N (weight). After the bodies collide, they keep moving together. Before we can calculate the common speed, we need to calculate the masses of the bodies, since they are given as weights.

`m_1=(P_1)/(g)=(1200)/(9.8)=122.45 Kg`

`m_2=(P_2)/(g)=(30)/(9.8)=3.06 Kg`

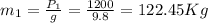
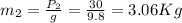
Now calculate the common speed:

`\displaystyle v'=(122.45 * 2+3.06 * 0)/(122.45+3.06)`

`\displaystyle v'=(244.9)/(125.51)=1.95\ m/s`

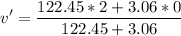
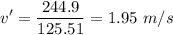
The common speed is 1.95 m/s