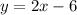Question

What is the equation in slope-intercept form of the linear function represented by the table?

6 -18
-1 I 8
42
9 12
O y=-2x-6
O y=-2x+6
O y = 2x--6
O y = 2x+6

Answer 1

`y=2x-6`

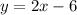
Explanation:

The equation of a line in slope-intercept form is
`y=mx+b`, where
`m` is the slope and
`b` is the y-intercept.

From the table, consider the last two points:

`(4,2)\textrm{ and }(9,12)`

The equation of the line using two points is given as:

`y-y_(1)=(y_(2)-y_(1))/(x_(2)-x_(1))(x-x_(1))`

Here,
`(x_(1),y_(1))=(4,2)\textrm{ and }(x_(2),y_(2))=(9,12)`

`y-2=(12-2)/(9-4)(x-4)\\ y-2=(10)/(5)(x-4)\\y-2=2(x-4)\\y-2=2x-8\\y=2x-8+2\\y=2x-6`

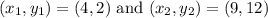
Therefore, the equation of the line in slope-intercept form is:

`y=2x-6`