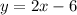Answer:
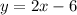
Explanation:
The equation of a line in slope-intercept form is
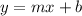 , where
, where
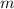 is the slope and
is the slope and
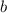 is the y-intercept.
is the y-intercept.
From the table, consider the last two points:
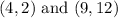
The equation of the line using two points is given as:
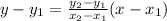
Here,
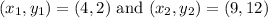
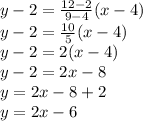
Therefore, the equation of the line in slope-intercept form is: