Answer: 271.4 s
Step-by-step explanation:
We are told the top speed (maximum speed)
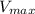 the car has is:
the car has is:
 taking into account
taking into account

And the car's average acceleration
 is:
is:
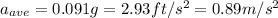
Since:
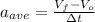 (1)
(1)
Where:
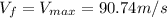 is the car's final speed (top speed)
is the car's final speed (top speed)
 because it starts from rest
because it starts from rest
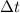 is the time it takes to reach the top speed
is the time it takes to reach the top speed
Finding this time:
 (2)
(2)
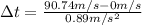 (3)
(3)
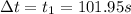 (4)
(4)
Now we have to find the distance
 the car traveled at this maximum speed with the following equation:
the car traveled at this maximum speed with the following equation:
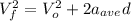 (5)
(5)
Isolating
 :
:
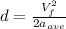 (6)
(6)
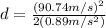 (7)
(7)
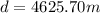 (8)
(8)
On the other hand, we know the total distance
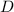 traveled by the car is:
traveled by the car is:
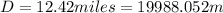
Hence the remaining distance is:
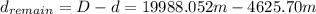 (9)
(9)
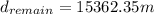 (10)
(10)
So, we can calculate the time
 it took to this car to travel this remaining distance
it took to this car to travel this remaining distance
 at its top speed
at its top speed
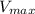 , with the following equation:
, with the following equation:
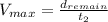 (11)
(11)
Isolating
 :
:
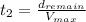 (12)
(12)
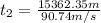 (13)
(13)
 (14)
(14)
With this time
 and the value of
and the value of
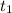 calculated in (4) we can finally calculate the total time
calculated in (4) we can finally calculate the total time
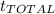 :
:
 (15)
(15)
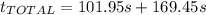 (16)
(16)
