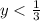For this case we have the following inequality:
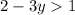
We solve by following the steps below:
We subtract 2 from both sides of the inequality:

Different signs are subtracted and the sign of the major is placed:
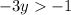
We divide between 3 on both sides of the inequality:
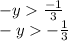
We multiply by -1 on both sides taking into account that the sense of inequality changes:
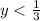
ANswer:
The solution is: