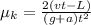Question

A student, along with her backpack on the floor next to her, are in an elevator that is accelerating upward with acceleration a. The student gives her backpack a quick kick at t = 0, imparting to it speed v and causing it to slide across the elevator floor. At time t, the backpack hits the opposite wall a distance L away from the student. Find the coefficient of kinetic friction μk between the backpack and the elevator floor. (Use any variable or symbol stated above along with the following as necessary: g.)

Answer 1

`\mu_k = (2(vt - L))/((g + a) t^2)`

Step-by-step explanation:

As we know that backpack is kicked on the rough floor with speed "v"

So here as per force equation in vertical direction we know that

`N - mg = ma`

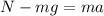
so normal force on the block is given as

`N = mg + ma`

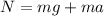
now the magnitude of kinetic friction on the block is given as

`F_f = \mu N`

`F_f = \mu (mg + ma)`

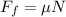
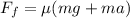
now when bag is sliding on the floor then net deceleration of the block due to friction is given as

`a = - (F_f)/(m)`

`a = -\mu_k(g + a)`

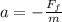
now we know that bag hits the opposite wall at L distance away in time t

so we have

`d = v t + (1)/(2)at^2`

`L = vt - (1)/(2)(\mu_k)(g + a) t^2`

`\mu_k = (2(vt - L))/((g + a) t^2)`