Question

A piece of cardboard is 1 meter by 1/21/2 meter. A square is to be cut from each corner and the sides folded up to make an open-top box. What are the dimensions of the box with maximum possible volume?

Answer 1

The maximum dimensions of the box:

Length of the box = 0.788676 m

Breadth of the box = 0.288676 m

Explanation:

Original piece of cardboard is a square with sides of length s.

Length of the card board = l = 1 m

Breadth of cardboard = b = 1/2 m = 0.5 m

Squares with sides of length x are cut out of each corner of a rectangular cardboard to form a box.

Now, length of the box = L = 1 - 2x

And breadth of the box = B = 0.5 - 2x

Height of the box ,H = x

Volume of the box ,V= L × B × H

`(dV)/(dx)=((1 -2x)(0.5-2x)x)/(dx)`

`(dV)/(dx)=(d(0.5x-3x^2+4x^3))/(dx)`

`(dV)/(dx)=0.5-6x+12x^2`

`(dV)/(dx)=O`

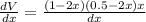
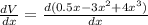
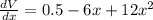
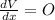
x = 0.394338 , 0.105662

`(d^2V)/((dx)^2)=-6+24x`

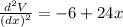
When ,
`x=0.105662` ,
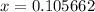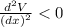`(d^2V)/((dx)^2)<0` (maxima)

The maximum dimensions of the box:

Length of the box = L = 1 - 2x = 1 - 2(0.105662) m = 0.788676 m

Breadth of the box = B = 0.5 - 2x = 0.5 - 2(0.105662) m = 0.288676 m