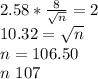Question

After a ham is cured it may be smoked to add flavor or to ensure it lasts longer. Typical grocery-store hams are smoked for a short period of time, whereas gourmet hams are usually smoked for at least one month. A random sample of 36 grocery-store hams was obtained, and the length of the smoking time was recorded for each. The mean was

hours. Assume σ = 8 hours.

a) What assumptions are required so that you can construct a confidence interval?
b) Find a 99% confidence interval for the for the mean amount of time a grocery-store

ham is smoked.
c) Interpret your answer in part b).
d) The precision required for someone in the deli who cooks the grocery store hams is a

margin of error (half-width) of 2 hours. How large a sample is necessary for this precision?

Answer 1

107

Explanation:

Given that after a ham is cured it may be smoked to add flavor or to ensure it lasts longer.

Let X be the smoking time . Then X is N(mu, 8)

a) The sample is drawn at random

b) The sample represents the population

c) Sample size is sufficient to represent the population

b)For 99% conf interval z critical is taken since population std dev is given

Z critical = 2.58

Hence confi interval =
`(\mu+/- 2.58*(\sigma)/(√(n) ) \\=(\mu +/- 2.58(8)/(6) )\\= (\mu -3.44, \mu+3.44)`

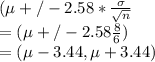
c) As sample sizes are large and samples are randomly drawn, we can be 99% confident that sample mean falls within this interval

d) If margin of error is only 2, then we must have

`2.58*(8)/(√(n) ) =2\\10.32=√(n) \\n=106.50\\n~107`