Answer:
0.8188 or 82%
0.0000643
Explanation:
Given that engineering specifications on the shelf depth of a certain slug to be turned on a CNC lathe are from .0275 in. to .0278 in.
If x is the dimension then X is N(0.0276, 0.0001)
Or
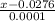 is Normal (0,1)
is Normal (0,1)
a) Fraction of shelf depths are in specifications
=
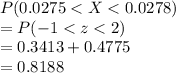
b) For 98% to be within the specifications,
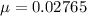
Margin of error =
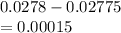
For 98% critical value Z two tailed is 2.33
Hence std error =
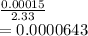
So sigma should be = 0.0000643