Question

If the product of two positive consecutive odd integers is 63, what’s the larger number ?

Answer 1

For this case we have:

`x`: Let the variable representing the first odd number

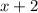`x + 2`: Let the variable representing the consecutive odd number at x.

According to the statement we have:

`x (x + 2) = 63\\x ^ 2 + 2x = 63\\x ^ 2 + 2x-63 = 0`

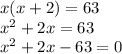
We found the solution by factoring:

We look for two numbers that, when multiplied, result in -63 and when added, result in 2. These numbers are +9 and -7.

`9-7 = 2\\9 * (-7) = -63`

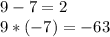
Thus, we have:

`(x + 9) (x-7) = 0`

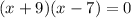
Therefore the solutions are:

`x_ {1} = - 9\\x_ {2} = 7`

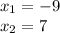
We choose the positive value, so we have:

`x = 7\\x + 2 = 7 + 2 = 9`

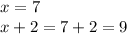
Answer:

The largest number is 9