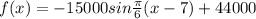Question

Over the past several years, the owner of a boutique on Aspen Avenue has observed a pattern in the amount of revenue for the store. The revenue reaches a maximum of about $ 59000 in April and a minimum of about $ 29000 in October. Suppose the months are numbered 1 through 12, and write a function of the form f(x)=Asin(B[x−C])+D that models the boutique's revenue during the year, where x corresponds to the month. If needed, you can enter π=3.1416... as 'pi' in your answer.

Answer 1

Explanation:

Given that the revenue reaches a maximum of about $ 59000 in April and a minimum of about $ 29000 in October. Suppose the months are numbered 1 through 12, where the months are numbered 1 through 12

Then minimum when x=10 and maximum when x = 4

Average = 44000 correspond to middle line

Amplitude =
`59000-44000 = 15000`

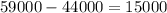
Hence the function roughly would be

`f(x) = 15000sin (B(X-C))+44000`

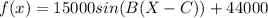
So we found out two values for A and D

To find values for B and C

The minimum of sine function corresponds to -pi/2 here it is 10 and maximum pi/2 here is 4.

Period = 12 months

So B = coefficient of X =
`(12)/(2\pi) \\=(6)/(\pi)`

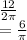
Because symmetrical about x=7 we have x-7 with a negative sign since min atx =10

`f(x) =-15000sin (\pi)/(6) (x-7)+44000`