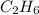Question

The heats of combustion of ethane (C2H6) and butane (C4H10) are 52 kJ/g and 49 kJ/g, respectively. We need to produce 1.000 x 103 kJ heat by burning one of the fuels. Which fuel will emit the least amount of CO2? 1. Calculate the number of grams needed of each fuel: 2. Calculate the number of moles of each fuel: 3. Write down the balanced chemical equation for the combustion of the fuels: 4. Calculate the number of moles of CO2 produced by burning each fuel to produce 1.000 x 103 kJ. Which fuel will emit the least amount of CO2?

Answer 1

(1) The number of grams needed of each fuel
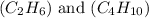`(C_2H_6)\text{ and }(C_4H_(10))` are 19.23 g and 20.41 g respectively.

(2) The number of moles of each fuel
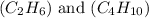`(C_2H_6)\text{ and }(C_4H_(10))` are 0.641 moles and 0.352 moles respectively.

(3) The balanced chemical equation for the combustion of the fuels.

`C_2H_6+(7)/(2)O_2\rightarrow 2CO_2+3H_2O`

`C_4H_(10)+(13)/(2)O_2\rightarrow 4CO_2+5H_2O`

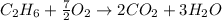
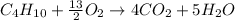
(4) The number of moles of
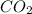`CO_2` produced by burning each fuel is 1.28 mole and 1.41 mole respectively.

The fuel that emitting least amount of
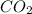`CO_2` is
`C_2H_6`

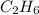
Explanation :

Part 1 :

First we have to calculate the number of grams needed of each fuel
`(C_2H_6)\text{ and }(C_4H_(10))`.

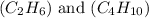As, 52 kJ energy required amount of
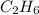`C_2H_6` = 1 g

So, 1000 kJ energy required amount of
`C_2H_6` =
`(1000)/(52)=19.23g`

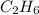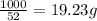
and,

As, 49 kJ energy required amount of
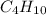`C_4H_(10)` = 1 g

So, 1000 kJ energy required amount of
`C_4H_(10)` =
`(1000)/(49)=20.41g`

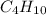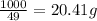
Part 2 :

Now we have to calculate the number of moles of each fuel
`(C_2H_6)\text{ and }(C_4H_(10))`.

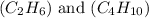Molar mass of
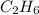`C_2H_6` = 30 g/mole

Molar mass of
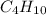`C_4H_(10)` = 58 g/mole

`\text{ Moles of }C_2H_6=\frac{\text{ Mass of }C_2H_6}{\text{ Molar mass of }C_2H_6}=(19.23g)/(30g/mole)=0.641moles`

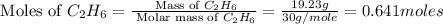
and,

`\text{ Moles of }C_4H_(10)=\frac{\text{ Mass of }C_4H_(10)}{\text{ Molar mass of }C_4H_(10)}=(20.41g)/(58g/mole)=0.352moles`

Part 3 :

Now we have to write down the balanced chemical equation for the combustion of the fuels.

The balanced chemical reaction for combustion of
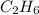`C_2H_6` is:

`C_2H_6+(7)/(2)O_2\rightarrow 2CO_2+3H_2O`

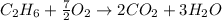
and,

The balanced chemical reaction for combustion of
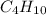`C_4H_(10)` is:

`C_4H_(10)+(13)/(2)O_2\rightarrow 4CO_2+5H_2O`

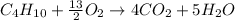
Part 4 :

Now we have to calculate the number of moles of
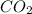`CO_2` produced by burning each fuel to produce 1000 kJ.

`C_2H_6+(7)/(2)O_2\rightarrow 2CO_2+3H_2O`

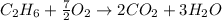
From this we conclude that,

As, 1 mole of
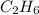`C_2H_6` react to produce 2 moles of
`CO_2`

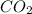
As, 0.641 mole of
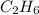`C_2H_6` react to produce
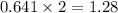`0.641* 2=1.28` moles of
`CO_2`

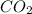
and,

`C_4H_(10)+(13)/(2)O_2\rightarrow 4CO_2+5H_2O`

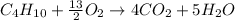
From this we conclude that,

As, 1 mole of
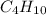`C_4H_(10)` react to produce 4 moles of
`CO_2`

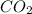
As, 0.352 mole of
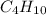`C_4H_(10)` react to produce
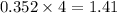`0.352* 4=1.41` moles of
`CO_2`

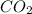
So, the fuel that emitting least amount of
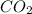`CO_2` is
`C_2H_6`