Answer:
P = 1162 W
E = 33 476 923 Joules
Step-by-step explanation:
Hi, to calculate the total power hitting the panel we must integrate the power density P(x,y) inside the panel area, that is:
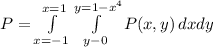
First we integrate the y variable since is the dependent variable for the present problem.
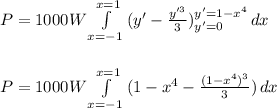
The integral is pretty straigthfoward, but involves expanding the binomial.
However the answer is:
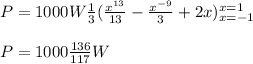
That is:
P = 1162 W
Since 1W = 1J/1s
The total energy recieved in 8 hours will be:
E = P*(8*3600 s)
E = 33 476 923 Joules