Question

A solar panel occupies the region bounded by y = 1 − x^4 and y = 0 (length units in meters). Suppose the power density of sunlight hitting the panel is P(x, y) = 1000 (1 − y/2) watts/m2 . Find the total power hitting the panel. How much energy (Joules) does the panel receive in 8 hours? (1 watt = 1 Joule/sec)

Answer 1

P = 1162 W

E = 33 476 923 Joules

Step-by-step explanation:

Hi, to calculate the total power hitting the panel we must integrate the power density P(x,y) inside the panel area, that is:

`P = \int\limits^(x=1)_(x=-1) \int \limits^(y=1-x^4)_(y-0) {P(x,y)}\, dxdy\\`

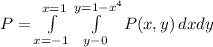
First we integrate the y variable since is the dependent variable for the present problem.

`P = 1000W\int\limits^(x=1)_(x=-1) {(y' - (y'^3)/(3))\limits^(y'=1-x^4)_(y'=0)} \, dx\\\\\\P= 1000W \int\limits^(x=1)_(x=-1) {(1-x^4 - ((1-x^4)^3)/(3))} \, dx`

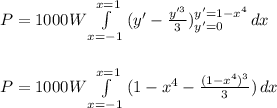
The integral is pretty straigthfoward, but involves expanding the binomial.

However the answer is:

`P = 1000W (1)/(3) ((x^(13) )/(13) - (x^(-9))/(3) +2x)\limits^(x=1)_(x=-1)\\\\P = 1000 (136)/(117) W`

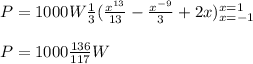
That is:

P = 1162 W

Since 1W = 1J/1s

The total energy recieved in 8 hours will be:

E = P*(8*3600 s)

E = 33 476 923 Joules