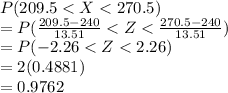Answer:
Explanation:
Given that about 24% of the Canadian population over 15 years of age are first generation; that is, they were born outside Canada.
X - first-generation Canadians in random samples of 1000 persons over 15 should therefore vary with the binomial (n = 1000, p = 0.24) distribution.
a) Mean of X =
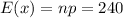
Var(x) =
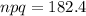
Standard deviation =
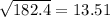
b) When approximated to normal this variable X will be normal
we check whether np and nq are greater than 5.
Here we find both are greater than 5. So binomial to normal approximation can be done.
X is N(240, 13.51)
the probability that the sample will contain between 210 and 270 first-generation Canadians
With continuity correction this equals