Answer:
Number of vines that should be planted are 150.
Explanation:
The number of pounds of pounds of grapes produced per acre is represented by the expression
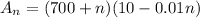
Where n = additional vines planted
To maximize the production of grapes we will find the derivative of A(n) and equate it to zero.
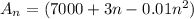
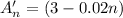
For
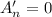
3 - 0.02n = 0
0.02n = 3
n =
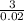
n = 150
To check whether the maximum value of the function is at n = 150, we will find the second derivative A(n).
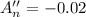
Which shows A"(n) < 0
Therefore, A(n) has the maximum value at n = 150.
Therefore, number of vines that should be planted are 150.