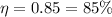Question

Water vapor at 5 bar, 320⁰ C enters a turbine operating at steady state with a volumetric flow rate of 0.65 m3 /s and expands adiabatically to an exit state of 1 bar, 160⁰ C. Kinetic and potential energy effects are negligible. Determine for the turbine

(a) the power developed, in kW
(b) the rate of entropy production, in kW/K
(c) the isentropic turbine efficiency.

Answer 1

Our values are given by,

`T_1 = 320\°cT_2 = 160\°c\\P_1 = 5 bar = 5000kPa\\P_2 = 1bar = 1000kPa\\\dot{V} = 0.65m^3/s\\`

From steam tables A5 we can calculate the values for State 1, that is,

`\\u_1 = 0.5416m^3/kg\\s_1 = 7.5308kJ/KgK\\h_1 = 3105.6kJ/kg`

Here is easily to find the flow mass rate, through

`\dot{m} = \frac{\dot{V}}{\\u_1}`

`\dot{m} = (0.65)/(0.5416) = 1.2kg/s`

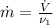
We apply a similar process to State 2, then

`s_2 = 7.6597kJ/kgK\\h_2 = 2796.2kJ`

With this values we can now calculate the Power, which is given by,

`P=\dot{m} (h_1-h_2) = 1.2(3105.6-2796.2)) = 371.28kW`

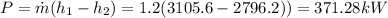
The total rate in entropy, that is

`\Delta S = \dot{m}(s_2-s_1) = 1.2 (7.6597-7.5308) = 0.1547kW/K`

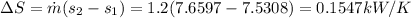
To find the efficiency we know that in a isentropic state, the entropy
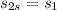`s_(2s) = s_1` then

`(h_(2s)-h_(120c))/(h_(160c)-h_(120c)) = (s_(2s)-s_(120c))/(s_(160c)-s_(120c))`

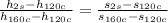
Replacing to find
`h_(2s)`

`(h_(2s)-2716.6)/(2796.2-2716.6)=(7.5308-7.4668)/(7.6597-7.4668)h_(2s)=2743.01kJ/kg`

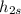
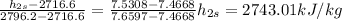
Then the efficiency is given by,

`\eta = (h_1-h_2)/(h_1-h_(2s)) = (3105.6-2796.2)/(3105.6-2743.01)`

`\eta = 0.85 = 85\%`