Question

Cholesterol levels for women aged 20 to 34 follow an approximately normal distributionwith mean 185 milligrams per deciliter (mg/dl). Women with cholesterol levels above 220 mg/dl are consid-ered to have high cholesterol and about 18.5% of women fall into this category. Find the standard deviationof this distribution of cholesterol levels for women aged 20 to 34?

Answer 1

The standard deviation of the distribution of cholesterol levels for women aged 20 to 34 is 39.019

Explanation:

If women with cholesterol levels above 220 mg/dl are considered to have high cholesterol and about 18.5% of women fall into this category, then

P(X>220)=0.185 From this probability, by looking z-table, z-statistic of a woman who has 220 mg/dl cholesterol level is 0.897.

z score for 220 mg/dl cholesterol level can also be calculated using the formula

z=
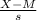`(X-M)/(s)` where

• X =220 mg/dl

• M is the mean cholesterol level for women aged 20 to 34 = 185 mg/dl

• s is the standard deviation of the distribution of cholesterol levels for women aged 20 to 34. Then

0.897=
`(220-185)/(s)` From this equation, we get s=39.019