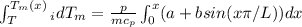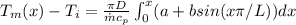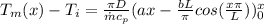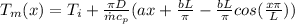Question

Consider a fluid with mean inlet temperature Ti flowing through a tube of diameter D and length L, at a mass flow rate m'. The tube is subjected to a surface heat flux that can be expressed as q(x)= a + bsin(xpi/L), where a and b are constants. Determine an expression for the mean temperature of the fluid as a function of the x-coordinate.

Answer 1

`T_m(x) = T_i+\frac{\pi D}{\dot{m}c_p}(ax+(bL)/(\pi)-(bL)/(\pi)cos((x\pi)/(L)))`

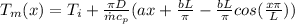
Step-by-step explanation:

Our data given are:

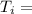`T_i =` Mean temperature (inlet)

D = Diameter

L = Length

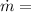`\dot{m}=`Mass flow rate

Equation to surface flow as,

`q(x) = a+bsin(x\pi/L)`

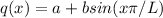
We need to consider the perimeter of tube (p) to apply the steady flow energy balance to a tube , that is

`q(x)pdx=\dot{m}c_p dT_m`

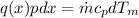
Where
`p=\pi D`

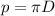
Re-arrange for
`dT_m,`

`dT_m = \frac{q(x)pdx}{\dot{m}c_p}`

Integrating from 0 to x (the distance intelt of pipe) we have,

`\int\limit^(T_m(x))_T_i dT_m = (p)/(mc_p)\int_0^x q(x)dx`

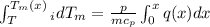
Replacing the value of q(x)

`\int\limit^(T_m(x))_T_i dT_m = (p)/(mc_p)\int_0^x (a+bsin(x\pi/L))dx`

`T_m(x)-T_i = \frac{\pi D}{\dot{m}c_p}\int_0^x(a+bsin(x\pi/L))dx`

`T_m(x)-T_i = \frac{\pi D}{\dot{m}c_p}(ax-(bL)/(\pi)cos((x\pi)/(L)))^x_0`

`T_m(x) = T_i+\frac{\pi D}{\dot{m}c_p}(ax+(bL)/(\pi)-(bL)/(\pi)cos((x\pi)/(L)))`