Answer:
a)
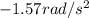 was the angular acceleration of the grinding wheel.
was the angular acceleration of the grinding wheel.
b)800 revolutions has made by the wheel during the time it was coming to rest
Step-by-step explanation:
Initial angular velocity of grinding wheel
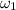 = 20.0 rps
= 20.0 rps
Final angular velocity of grinding wheel
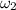 = 0.0 rps
= 0.0 rps
Time taken by wheel to come to rest = t = 80.0 s
a) Angular acceleration of the wheel =

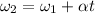

 revolutions per second square
revolutions per second square
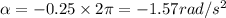
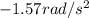 was the angular acceleration of the grinding wheel.
was the angular acceleration of the grinding wheel.
b) Initial angular velocity of grinding wheel
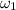 = 20.0 rps
= 20.0 rps
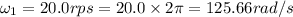
Number of revolution before coming to rest =
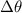

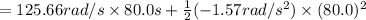
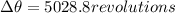
Number of revolution =
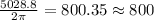
800 revolutions has made by the wheel during the time it was coming to rest