Question

The owner of a landscaping company is developing a proposal to maintain the grounds of a building. It is estimated that 75 gardening hours and 25 foreman hours will be required. The total budget for these hours is $1600. The hourly wage for a foreman is 30%, more than a gardener plus an additional $1.65 per hour. Which of the following systems of equations can be used to determine the hourly wages of a gardener, g, and a foreman, f, so the total wages are $1600?A. 25g+75f=1600 f=1.3g+1.65B. 25f+75g=1600

f=1.3g+1.65
C.25g+75f=1600
g=1.3f+1.65
D. 25f+75g=1600
g=1.3f+1.65

Answer 1

B

Explanation:

Answer 2

B

Explanation:

Given:

The estimated gardening hours = 75 hours

The estimated foreman hours = 25 hours

The hourly wages of a gardener = g

The hourly wages of a foreman = f

If the hourly wage for a foreman is 30%, more than a gardener plus an additional $1.65 per hour, then,

f = (
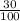`(30)/(100)` of g + g) + 1.65

f = (
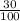`(30)/(100)` x g + g) + 1.65

f = 0.3g + g + 1.65

f = 1.3g + 1.65 (1)

The total wages for the gardeners = The estimated gardening hours x The hourly wages of a gardener

The total wages for the gardeners = 75 x g

= 75g

The total wages for the foreman = The estimated foreman hours x The hourly wages of a foreman

The total wages for the foreman = 25 x f

= 25f

The total wages for the foreman + The total wages for the gardeners = The total budgets for the project for the estimated hours

25f + 75g = 1600 (2)

Therefore the answer is option B. 25f + 75g = 1600 f = 1.3g + 1.65