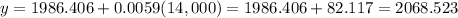Question

Consider this scenario: The population of a city increased steadily over a ten-year span. The following ordered pairs show the population x and the year y over the ten-year span in the form(x, y)for specific recorded years. Use linear regression to determine a function y, where the year depends on the population. Round to three decimal places of accuracy.(2500, 2001), (2650, 2002), (3000, 2004), (3500, 2007), (4200, 2011)Predict when the population will hit 14,000.The linear regression model based on this data predicts that this will happen during the year. So, y= ___ .

Answer 1

Regression function:
`y=1986.406+0.0059x`

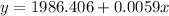
The function predicts that population will reach 14,000 in year 2068.

Explanation:

We have to determine a function
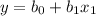`y=b_0+b_1x_1` by applying linear regression. The data we have is 5 pair of points which relates population to year.

According to the simple regression model (one independent variable), if we minimize the error between the model (the linear function) and the points given, the parameters are:

`b_0=\bar{y}+b_1\bar{x}\\\\b_1=\frac{\sum\limits^5_(i=1) {(x_i-\bar x)(y_i-\bar y)}}{\sum\limits^5_(i=1) {(x_i-\bar x)^2}}`

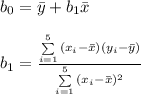
We start calculating the average of x and y

`\bar x=(2500+2650+3000+3500+4200)/(5)=(15850)/(5)=3170\\\\ \bar y=(2001+2002+2004+2007+2011)/(5)=(10025)/(5)=2005`

The sample covariance can be calculated as

`\sum\limits^5_(i=1) {(x_i-\bar x)(y_i-\bar y)}=(2500-3170)(2001-2005)+(2650-3170)(2002-2005)+(3000-3170)(2004-2005)+(3500-3170)(2007-2005)+(4200-3170)(2011-2005)\\\\\sum\limits^5_(i=1) {(x_i-\bar x)(y_i-\bar y)}=2680+1560+170+660+6180</p><p>\\\\ \sum\limits^5_(i=1) {(x_i-\bar x)(y_i-\bar y)}=11250`

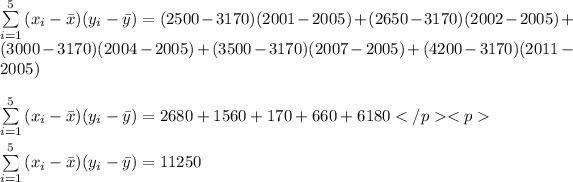
The variance of x can be calculated as

`\sum\limits^5_(i=1) {(x_i-\bar x)^2}=(2500-3170)^2+(2650-3170)^2+(3000-3170)^2+(3500-3170)^2+(4200-3170)^2\\\\\sum\limits^5_(i=1) {(x_i-\bar x)^2}=448900+270400+28900+108900+1060900</p><p>\\\\\sum\limits^5_(i=1) {(x_i-\bar x)^2}=1918000</p><p>`

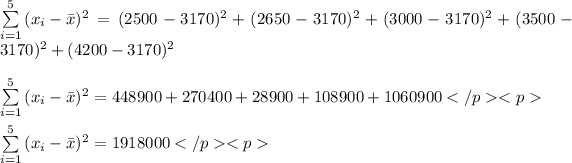
Now we can calculate the parameters of the regression model

`b_1=\frac{\sum\limits^5_(i=1) {(x_i-\bar x)(y_i-\bar y)}}{\sum\limits^5_(i=1) {(x_i-\bar x)^2}}=(11250)/(1918000)=0.005865485  \\\\ b_0=\bar{y}+b_1\bar{x}=2005-0.005865485*3170=1986.406413</p><p>`

The function then become:

`y=1986.406+0.0059x`

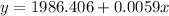
With this linear equation we can predict when the population will reach 14,000:

`y=1986.406+0.0059(14,000)=1986.406+82.117=2068.523`