Question

As the financial consultant to a classic auto dealership, you estimate that the total value (in dollars) of its collection of 1959 Chevrolets and Fords is given by the formula v = 301,000 + 960t2 (t ≥ 5) where t is the number of years from now. You anticipate a continuous inflation rate of 5% per year, so that the discounted (present) value of an item that will be worth $v in t years' time is p = ve−0.05t. When would you advise the dealership to sell the vehicles to maximize their discounted value? (Round your answer to one decimal place.) years from now

Answer 1

The owner will maximize value if it waits 29th years Assuming 5% continuos inflation

Step-by-step explanation:

the price formula for the future years is:

`v = 301000 + 960 t^(2)`

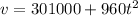
while it is adjusted for inflation at:

`v * e^(-0.05t)`

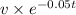
so the complete formula for value is:

`(301000 + 960 t^(2))/(e^(0.05t))`

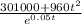
Now, we can derivate and obtain the roots

Getting at a root exist at the 29th year.

The owner will maximize value if it waits 29th years Assuming 5% continuos inflation