Question

Solve 3x - 4 ≤ 2 or 2x + 11 ≥ -1

Answer 1

The solution is all real numbers

Explanation:

we have the system of inequalities

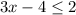`3x-4\leq 2` -----> inequality A

or

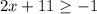`2x+11\geq -1` ----> inequality B

step 1

Solve inequality A

Adds 4 both sides

`3x\leq 2+4`

`3x\leq 6`

Divide by 3 both sides

`x\leq 2`

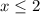
The solution is the interval ----> (-∞,2]

step 2

Solve inequality B

Subtract 11 both sides

`2x\geq -1-11`

`2x\geq -12`

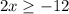
Divide by 2 both sides

`x\geq -6`

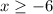
The solution is the interval ----> [-6,∞)

step 3

Find out the solution of the system of inequalities

The solution of the system is equal to the solution inequality A plus the solution of the inequality B (because the system has included the word "or")

so

[-6,∞) ∪ (-∞,2]=(-∞,∞)

The solution is all real numbers